13 Khiin neliö \(\chi^2\)
Mittausasteikot: Molemmat muuttujat luokittelu- tai järjestysasteikolla.
Khiin neliö tai khii kahteen, \(\chi^2\), on riippuvuusmitta jota voidaan käyttää kun molemmat muuttujat ovat kategorisia, eli luokittelu- tai järjestysasteikolla. Khiin neliössä käytetään vain muuttujien kategorioiden määriä \(n\).
Mitassa vertaillaan todellisia, mitattuja arvoja odotettuihin arvoihin: kuinka paljon dataa odottaisimme jokaisen kategoriaparin kohdalla esiintyvän, jos suhdetta muuttujien välillä ei ole?
Khiin neliössä lasketaan kaksi ristiintaulukointia: todelliset arvot ja odotetut arvot. Todelliset arvot saadaan yksinkertaisesti ristiintaulukoimalla molemmat muuttujat. Riippuvainen muuttuja laitetaan yleisesti sarakkeisiin ja riippumaton muuttuja riveihin, mutta laskutoimituksen kannalta tällä ei ole merkitystä. Todellisille arvoille lasketaan myös rivi- ja sarakesummat, sekä kokonaissumma (datapisteiden määrä).
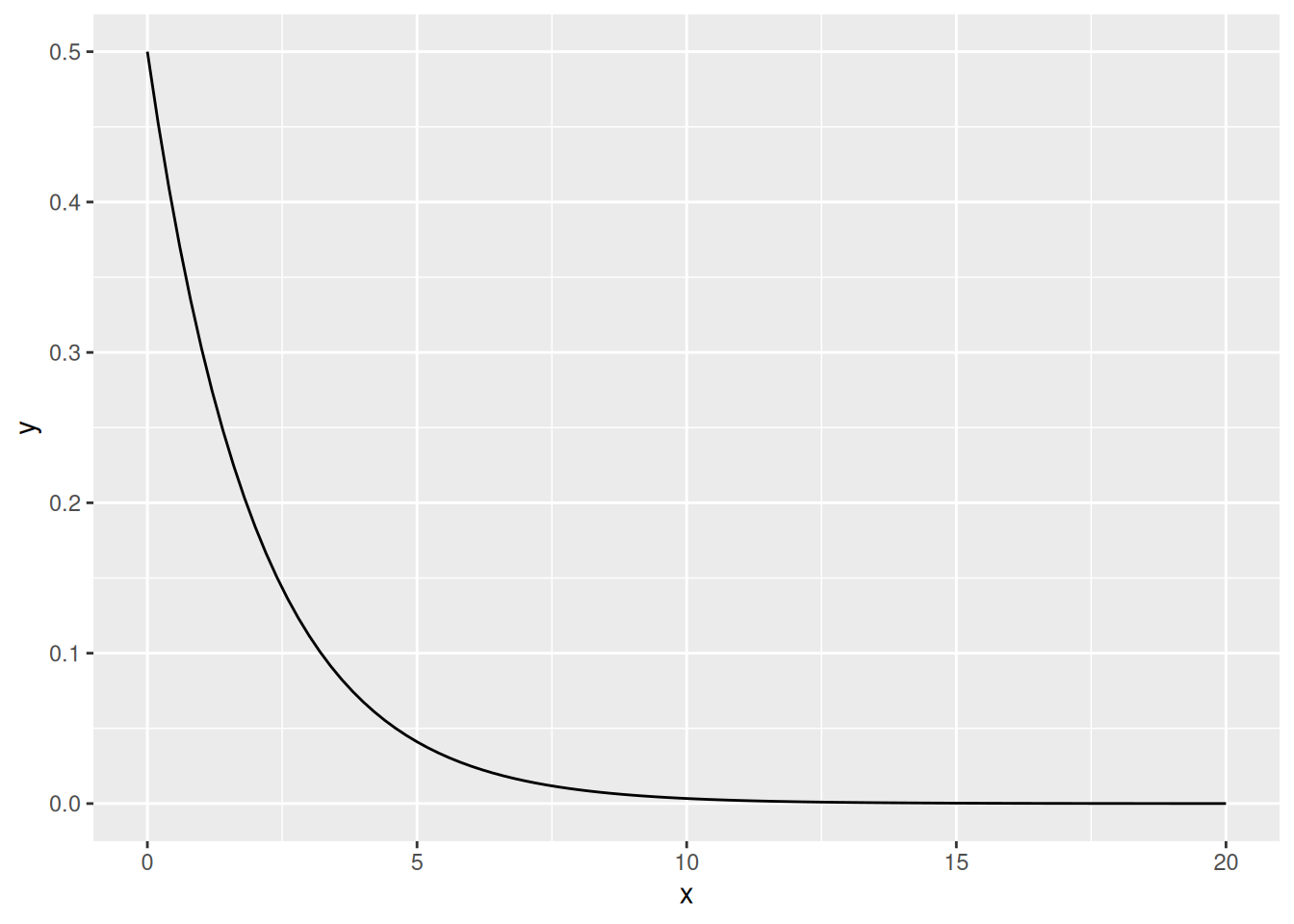
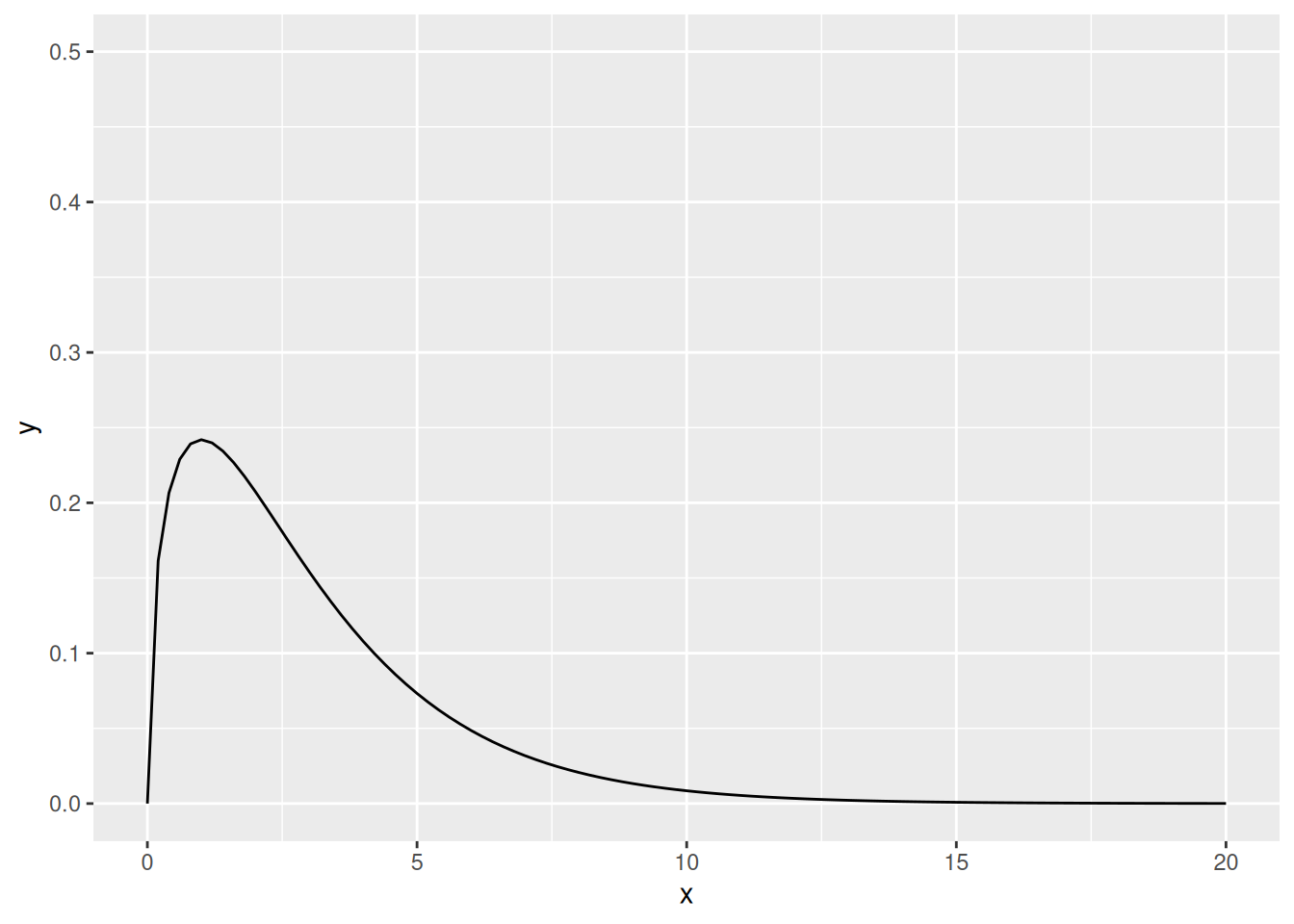
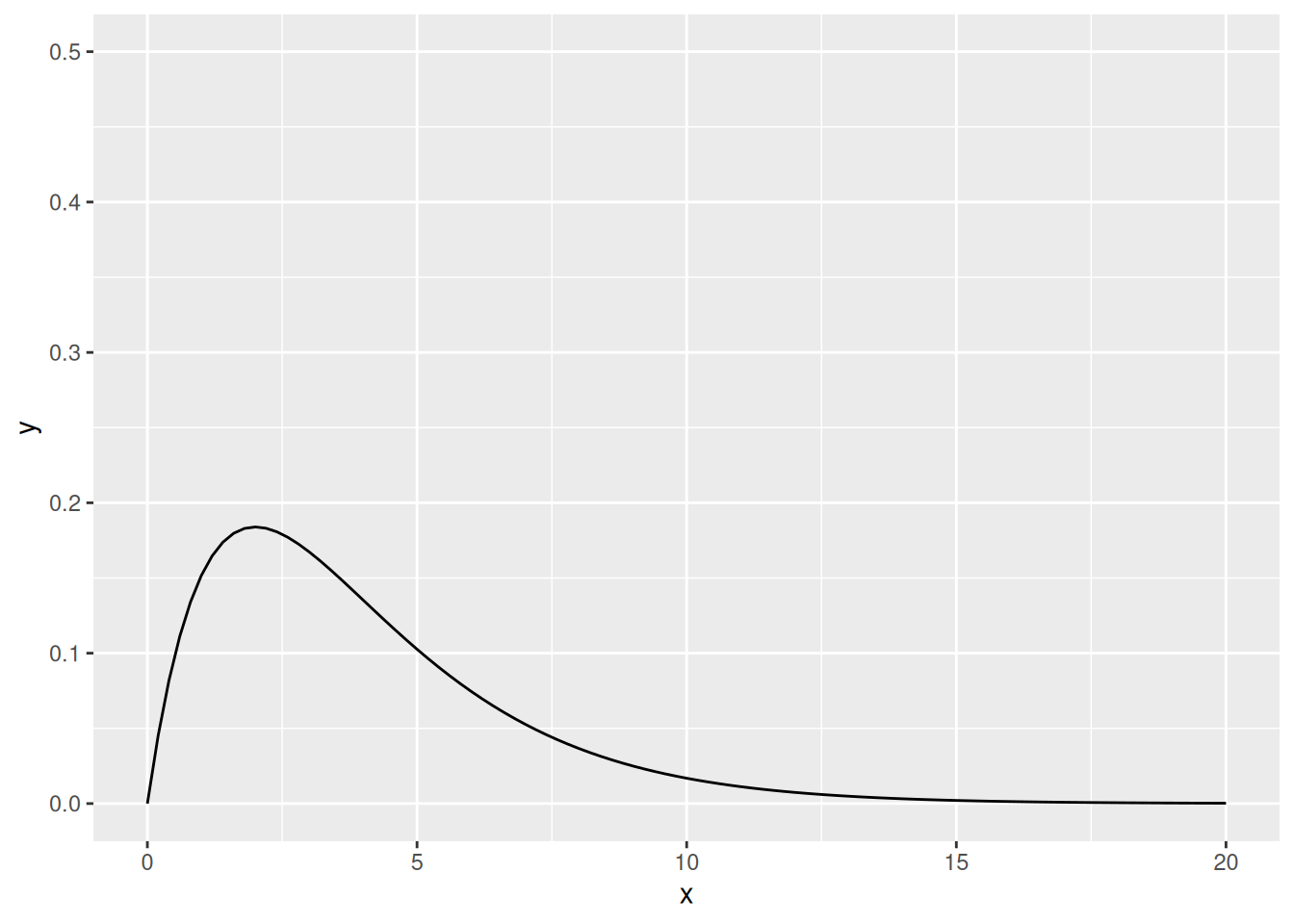
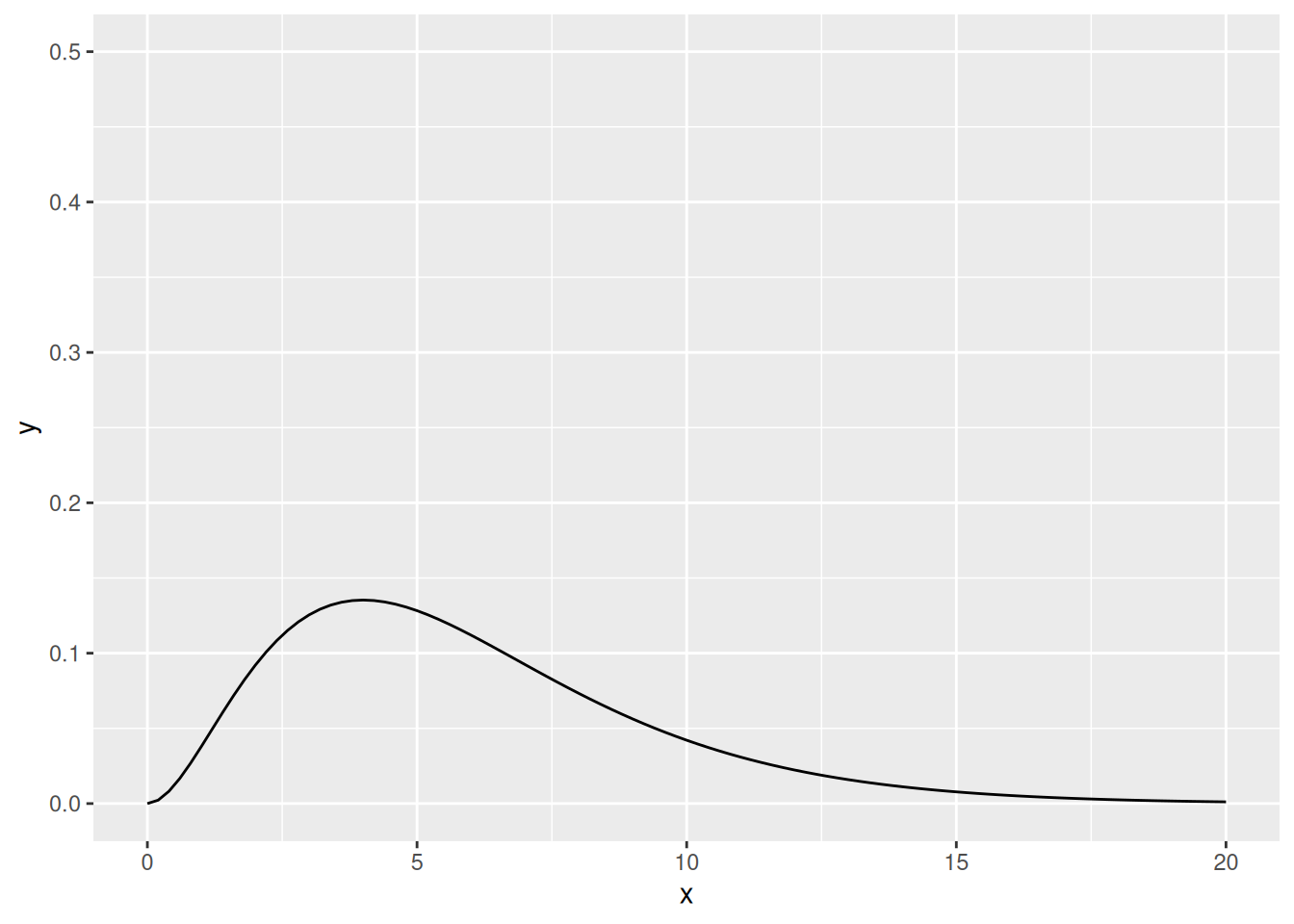
Khiin neliön suure vaihtelee nollasta (ei yhteyttä) äärettömään (täydellinen yhteys). Jakauman muoto määrittyy vapausasteista.
13.1 Khiin neliön malliodotukset
Khiin neliö ei riipu yleisistä malliodotuksista. Sen sijaan sillä on kaksi tärkeää omaa odotusta, liittyen riippumattomuuteen sekä odotettuihin arvoihin.
Riippumattomuudella tarkoitetaan tässä, että khiin neliö voidaan vain laskea ryhmien välisessä rakenteessa. Kahdessa kategoriassa ei siis voi olla samoja vastaajia. Jokaisen kategorian vastaaja tulisi olla uniikki yhdellä muuttujalla.
Solujen odotettujen arvojen minimimäärä on myös määritelty, jotta khiin neliön testi olisi luotettava. Jos testaat 2*2-rakennetta (eli molemmat muuttujat ovat dikotomisia), yksikään solu ei saisi saada odotetun arvon alle viisi. Jos testaat suurempaa rakennetta, kaikkien odotettujen arvojen tulisi olla yli yhden, ja korkeintaan 20 prosenttia (viidesosa) kaikista odotetuista arvoista saisi olla alle viiden.
Jos vaatimus ei täyty, sinulla on liian vähän dataa jokaisessa solussa laskeaksesi khiin neliön testin. Jos sinulla on useampia kategorioita jollain muuttujalla, voit yrittää yhdistellä niitä - mutta ota huomioon tulkittavuus! Voit myös kokeilla ei-parametrista testiä.
Huomioi myös, että suurissa otoksissa myös pienet erot voivat johtaa merkitsevään khiin neliön suureeseen. Tarkista aina erojen todelliset koot (prosenteissa tai absoluuttisissa arvoissa), jotta pystyt tulkitsemaan mahdollisen eron käytännön merkityksen.
13.2 Khiin neliön laskeminen
Nimetään solu rivien \(i\) ja sarakkeiden \(j\) mukaan. Todellinen arvo nimetään \(O_{ij}\) (engl. observed value) ja odotettu arvo nimetään \(E_{ij}\) (engl. expected value).
Todelliset arvot ovat yksinkertaisesti jokaisen solun esiintymämäärä, eli kuinka monta vastaajaa/yksikköä kuuluvat jokaiseen muuttujayhdistelmään.
Odotetut arvot lasketaan jokaiselle solulle \(ij\) laskukaavalla:
\[ E_{ij} = \frac{\text{rivisumma}_i * \text{sarakesumma}_j}{n} \tag{13.1}\]
Jokaisen solun \(ij\) kohdalla kerrotaan siis ensin solun rivisumma \(\sum{}_i\) solun sarakesummalla \(\sum{}_j\), jonka jälkeen tulos jaetaan kokonaissummalla \(n\). Lopputulos on odotettu arvo \(E_{ij}\).

Tämän jälkeen khiin neliö lasketaan jokaiselle solulle laskukaavalla:
\[ \chi^2_{ij} = \frac{(O_{ij} - E_{ij})^2}{E_{ij}} \tag{13.2}\]
Jokaisen solun \(ij\) kohdalla vähennetään siis ensin solun odotettu arvo \(E_{ij}\) solun todellisesta arvosta \(O_{ij}\). Tulos nostetaan neliöön, jonka jälkeen arvo jaetaan vielä odotetulla arvolla \(E_{ij}\).
Sitten summataan jokaisen solun khiin neliön arvo yhteen, jolloin saadaan khiin neliön suure, \(\chi^2\).
Khiin neliön suure noudattaa khiin neliön jakaumaa. Todennäköisyys merkitsee siksi todennäköisyyttä saada nähty khiin neliön suure tai isompi, jos populaatiossa khiin neliön arvo pitäisi olla nolla (ei yhteyttä).
Khiin neliön jakauma määritellään vapausasteilla. Khiin neliön vapausasteet on yksinkertaisesti rivien määrä minus yksi \(r-1\), kertaa sarakkeiden määrä minus yksi \(c-1\):
\[ \text{df} = (r - 1)(c - 1) \tag{13.3}\]
Khiin neliö voidaan raportoida sellaisenaan, mutta yleensä haluamme myös jonkun mitan siitä, kuinka suuri yhteys muuttujilla näyttäisi olevan. Paras vaihtoehto on tietenkin raportoida alkuperäiset todelliset arvot (tai niiden prosenttiosuudet), koska nämä ovat helpoimmin ymmärrettävissä.
Vaihtoehtoisesti voi myös käyttää Cramérin V-suuretta. V-suure vaihtelee nollasta yhteen, ja osoittaa yhdellä numerolla, kuinka laajasti muuttujat yhteisvaihtelevat. V-suure lasketaan kaavalla:
\[ V = \sqrt{\frac{\chi^2}{(min(r, c)-1)n}} \tag{13.4}\]
Ensin haet pienimmän rivi- tai sarakemääristä, ja vähennät siitä yhden. Kerrot tuloksen otoskoolla, eli kaikkien todellisten arvojen summalla. Sitten jaat khiin neliön suureen tällä tuloksella, ja otat laskennan tuloksen neliöjuuren. Lopputulos on Cramérin V-suure.
Cramérin V-suureen tulkinta riippuu vapausasteista. Taulukko alla näyttää raja-arvot tulkinnalle yleisimmille vapausasteille:
| Vapausaste | Pieni | Keski | Suuri |
|---|---|---|---|
| 1 | 0,1 | 0,3 | 0,5 |
| 2 | 0,07 | 0,21 | 0,35 |
| 3 | 0,06 | 0,17 | 0,29 |
| 4 | 0,05 | 0,15 | 0,25 |
| 5 | 0,04 | 0,13 | 0,22 |
13.3 Khiin neliö Excelissä
Khiin neliö vaatii neljä osa-askelta Excelissä:
- Todellisten arvojen taulukko,
- Odotettujen arvojen taulukko,
- Khiin neliön taulukko, ja
- Lopputuloslaskut.
13.3.1 Todellisten arvojen taulukko
- Hae muuttujien kategoriat riveihin ja sarakkeisiin:
- Rivit:
=LAJITTELE(AINUTKERTAISET.ARVOT(muuttuja1);;1) - Sarakkeet:
=TRANSPONOI(LAJITTELE(AINUTKERTAISET.ARVOT(muuttuja2);;1))
- Rivit:
- Laske todellisten arvojen määrät soluihin:
=LASKE.JOS.JOUKKO(muuttuja1; arvo1; muuttuja2; arvo2)- Voit käyttää arvoja suoraan muuttujien rivi- ja sarakelistauksista. Lukitse tuolloin sarakeviittaus rivimuuttujalle ja riviviittaus sarakemuuttujalle. Jos rivimuuttuja on soluissa
C6:C9ja sarakemuuttuja soluissaD5:H5, viittaa niiden ensimmäisten kategorioiden yhdistelmään arvoilla$C6jaD$5. - Vedä laskukaavio koko ristiintaulukoinnin alueelle vetotoiminnolla. Jos lukitsit yllä olevalla tavalla, kaikki laskennat pitäisi mennä oikein. Tarkista laskut!
- Voit käyttää arvoja suoraan muuttujien rivi- ja sarakelistauksista. Lukitse tuolloin sarakeviittaus rivimuuttujalle ja riviviittaus sarakemuuttujalle. Jos rivimuuttuja on soluissa
- Laske rivi- ja sarakesummat
SUMMA-funktiolla. - Laske kokonaissumma (otoskoko) summaamalla joko rivi- tai sarakesummat yhteen - ei molempia!
13.3.2 Odotettujen arvojen taulukko
- Hae taas muuttujien kategoriat riveihin ja sarakkeisiin:
- Rivit:
=LAJITTELE(AINUTKERTAISET.ARVOT(muuttuja1);;1) - Sarakkeet:
=TRANSPONOI(LAJITTELE(AINUTKERTAISET.ARVOT(muuttuja2);;1))
- Rivit:
- Laske odotettujen arvojen määrät soluihin:
=(sarakesumma * rivisumma) / kokonaissumma.- Voit jälleen käyttää arvoja rivi- ja sarakelistauksista. Lukitse sarakesummasta rivi, rivisummasta sarake, ja kokonaissummasta molemmat. Jos esim. sarakesummasi ovat alueella
D10:H10, rivisummasi alueellaI6:I9, ja kokonaissummasi solussaI10, viittaa silloin niihin lukituksillaD$10(sarakesumma),$I6(rivisumma) ja$I$10(kokonaissumma. - Vedä laskukaavio koko ristiintaulukoinnin alueelle. Jos lukitsit yllä olevalla tavalla, kaiken pitäisi taas olla oikein. Tarkista laskut!
- Voit jälleen käyttää arvoja rivi- ja sarakelistauksista. Lukitse sarakesummasta rivi, rivisummasta sarake, ja kokonaissummasta molemmat. Jos esim. sarakesummasi ovat alueella
13.3.3 Khiin neliön taulukko
- Hae vielä kerran muuttujien kategoriat riveihin ja sarakkeisiin:
- Rivit:
=LAJITTELE(AINUTKERTAISET.ARVOT(muuttuja1);;1) - Sarakkeet:
=TRANSPONOI(LAJITTELE(AINUTKERTAISET.ARVOT(muuttuja2);;1))
- Rivit:
- Laske jokaiselle solulle oma khiin neliön arvo:
=(todellinen_arvo - odotettu_arvo) ^ 2 / odotettu_arvo- Et tarvitse lukita mitään.
- Vedä laskukaavio koko ristiintaulukoinnin alueelle.
13.3.4 Lopputuloslaskut
- Laske khiin neliön suure:
=SUMMA(khiin_neliön_taulukko) - Laske otoskoko:
=kokonaissumma(ei sinänsä tarpeellista, mutta taulukoiden lukeminen on helpompaa jos kaikki tarvittavat tilastot löytyvät samasta paikasta) - Laske alle viiden odotettujen arvojen määrä:
=SUMMA(JOS(odotetut_arvot_taulukko < 5; 1; 0)). Voit myös laskea niiden prosenttimäärän:=alle_viisi/LASKE(odotetut_arvot_taulukko)% - Laske myös alle yhden odotettujen arvojen määrä:
=SUMMA(JOS(odotetut_arvot_taulukko < 1; 1; 0)). Voit jälleen laskea niiden prosenttimäärän:=alle_yhden/LASKE(odotetut_arvot_taulukko)% - Laske rivien ja sarakkeiden määrät. Voit tehdä tämän käsin - näihin lukuihin viittaaminen helpottaa seuraavia laskukaavoja hieman.
- Laske khiin neliön vapausasteet:
=(rivimäärä - 1) * (sarakemäärä - 1) - Hae khiin neliön suureen todennäköisyys:
=CHINELIÖ.JAKAUMA.OH(khiin_neliö; vapausasteet) - Laske Cramérin V-suure:
=NELIÖJUURI(khiin_neliö / ((MIN(rivimäärä; sarakemäärä) - 1) * otoskoko))
13.4 Khiin neliön raportointi
Khiin neliön testistä raportoidaan mieluisesti seuraavat tiedot:
Testisuure \(\chi^2\)
Vapausasteet \(\text{df}\)
P-arvo \(p\)
Kuinka moni odotettu arvo on alle 1 tai alle 5 (ks. Alaluku 13.1)
Jos laskettu: Cramérin V-suure \(V\)
Cramerin V-suure voidaan tulkita jokseenkin samoin kuin Cohenin \(\hat{d}\) tai Pearsonin \(r\), mutta tulkinta riippuu osittain vapausasteista:
| Vapausaste | Pieni koko | Keskikokoinen | Suuri koko |
|---|---|---|---|
| 1 | 0,1 | 0,3 | 0,5 |
| 2 | 0,07 | 0,21 | 0,35 |
| 3 | 0,06 | 0,17 | 0,29 |
| 4 | 0,05 | 0,15 | 0,25 |
| 5 | 0,04 | 0,13 | 0,22 |
Yleensä kannattaa myös jatkoanalysoida mitkä kategoriat eroavat toisistaan, esimerkiksi post hoc-testeillä. Voit myös tarkastaa solujen prosenttiosuuksia ja raportoida isoimmat erot, mutta tämä ei ole yhtä luotettava menetelmä kuin virallinen testaus.
Prontoon kirjatuissa asuntopaloissa havaittiin suuri, merkitsevä yhteys rakennuksen riskiluokituksen ja palovaroittimen toiminnan välillä (\(\chi^2 = 29.3\), \(\text{df} = 9\), \(p = 0.0006\), \(V = 0.22\)). Riskiluokkaan 1 kuuluvista rakennuksista jopa 56 prosentilla puuttui palovaroitin, kun vastaava arvo muissa riskiluokissa oli 18 - 33 prosenttia. Palovaroittimen toiminta oli harvinaisinta riskiluokka 4:ssä (7 %). Kaikki odotetut arvot ylittivät yhden, mutta kolme solua (19 %) olivat alle viiden. Tulokset ovat siten tulkittavuuden rajalla, ja voivat olla väärällisiä.
